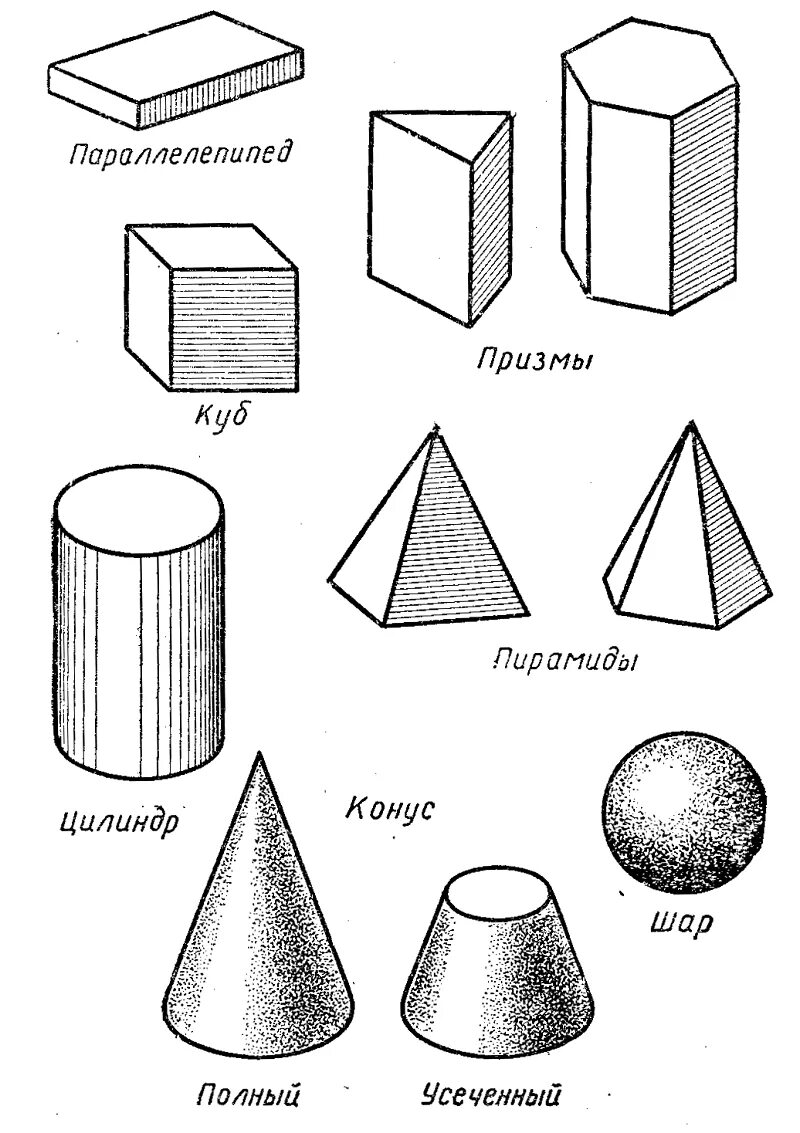
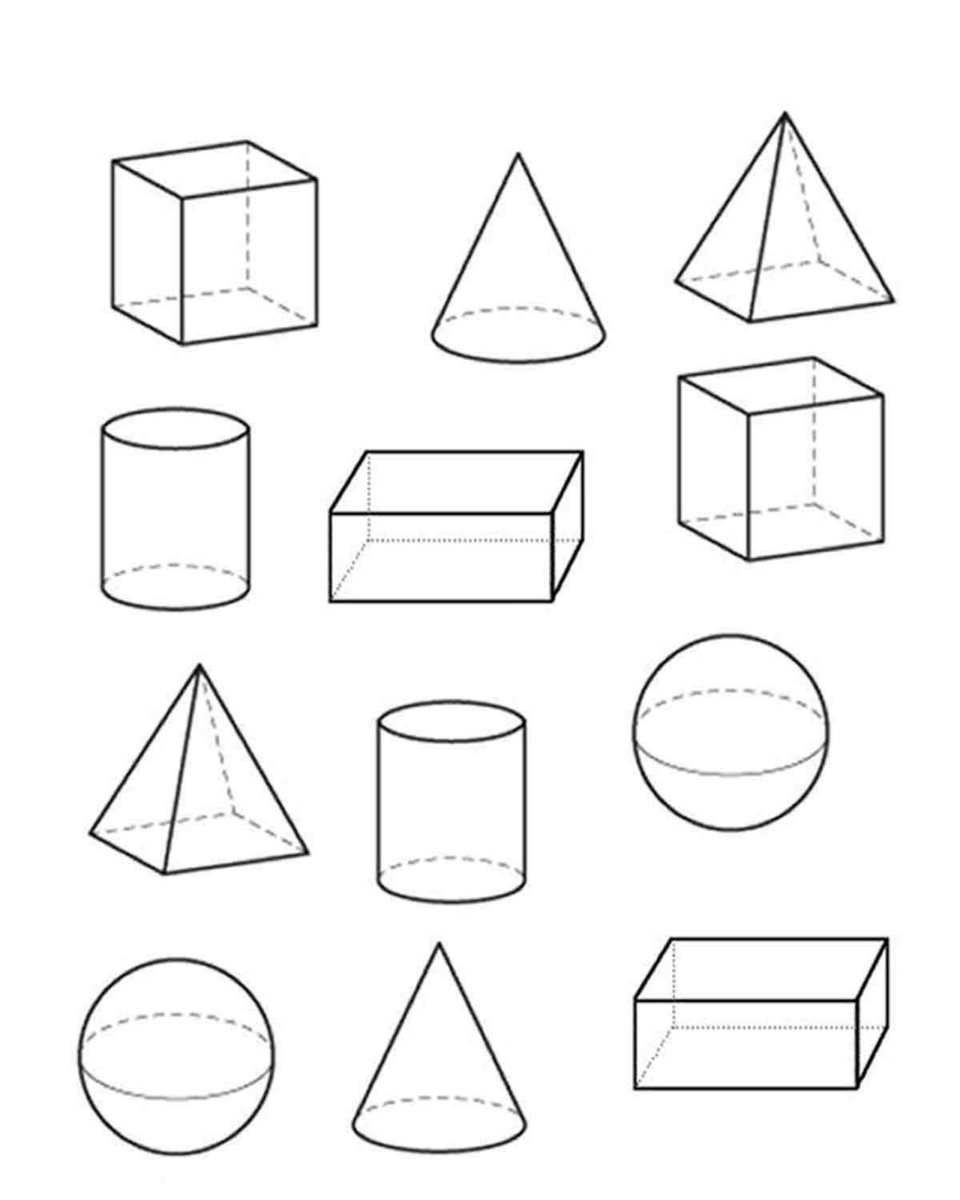
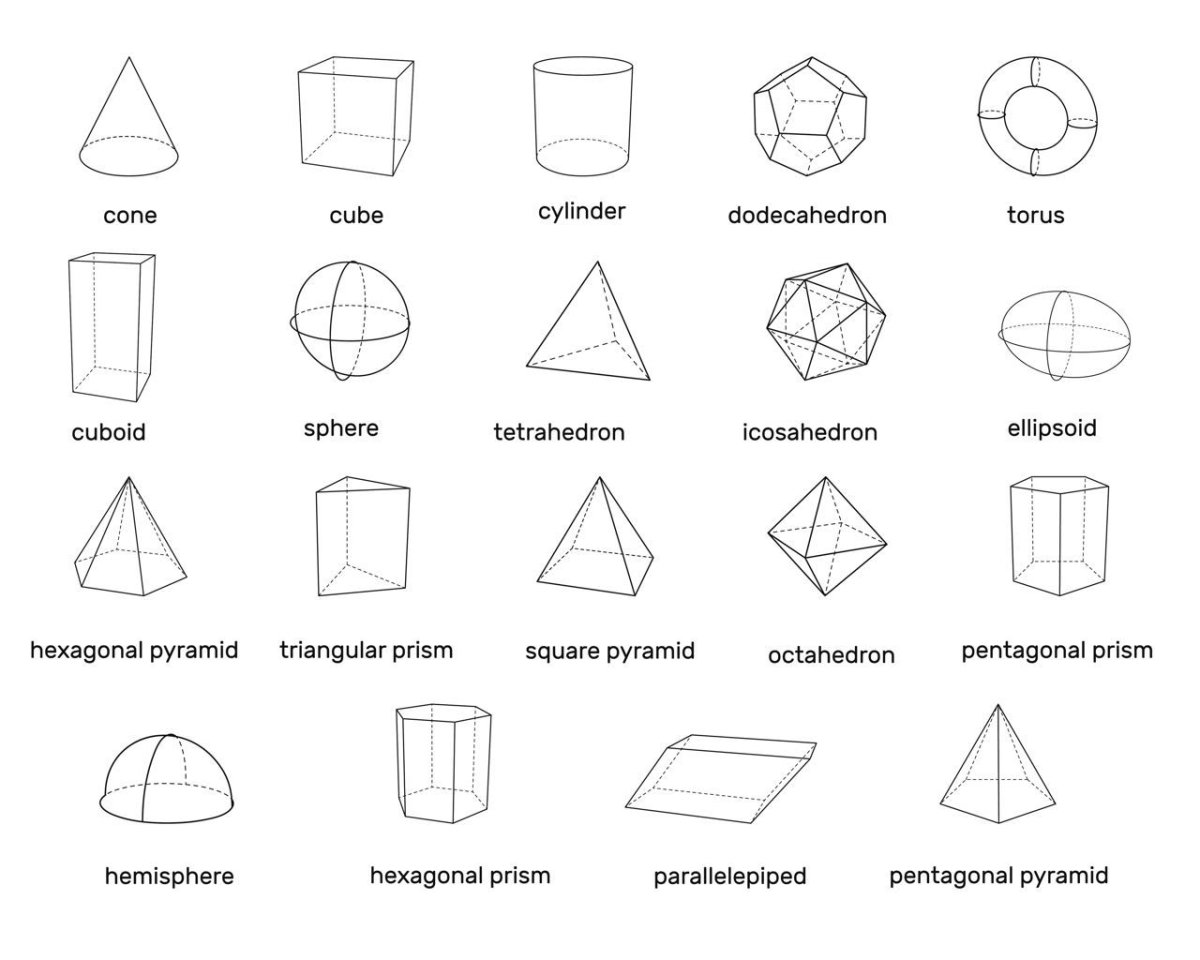
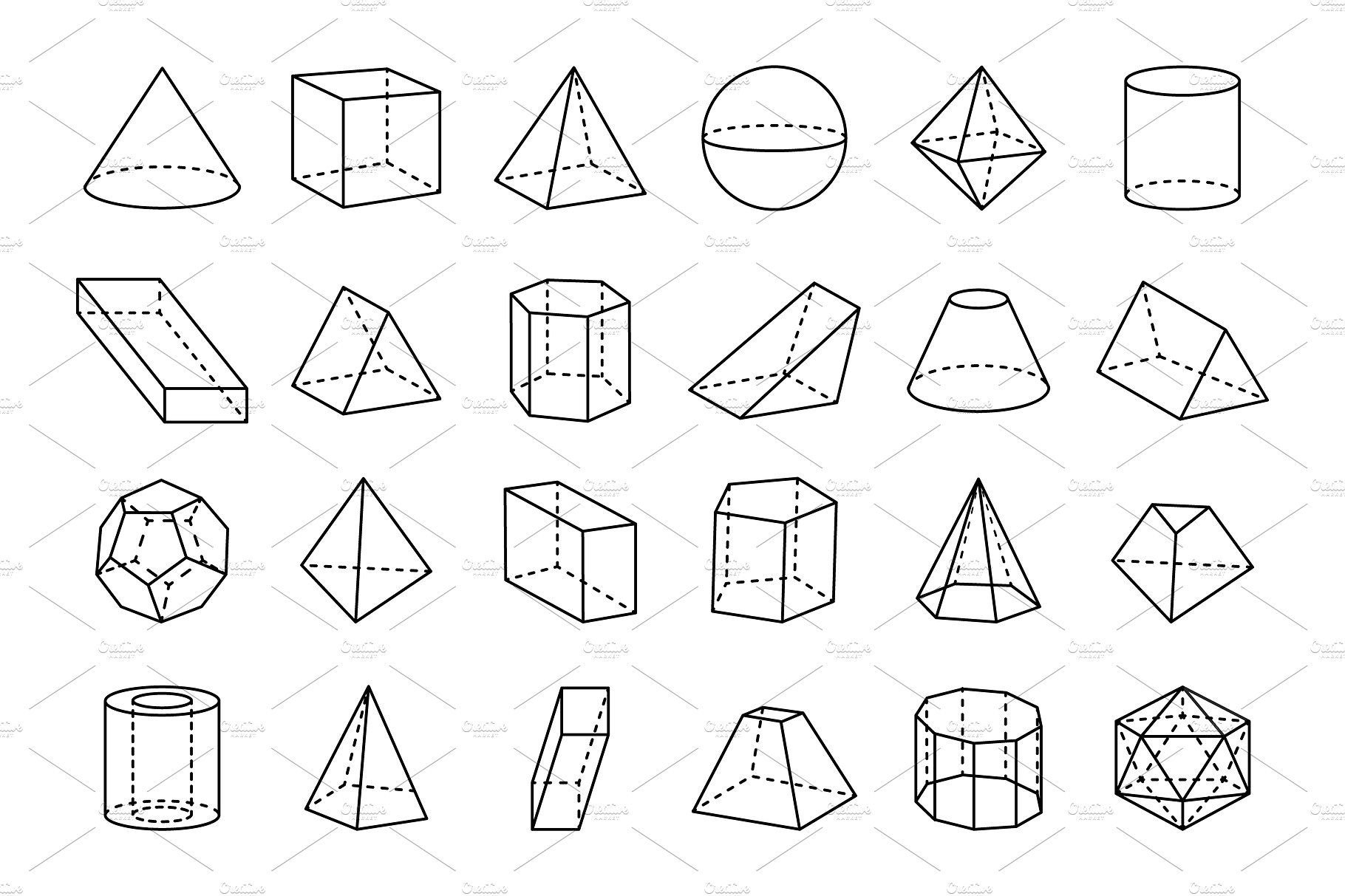
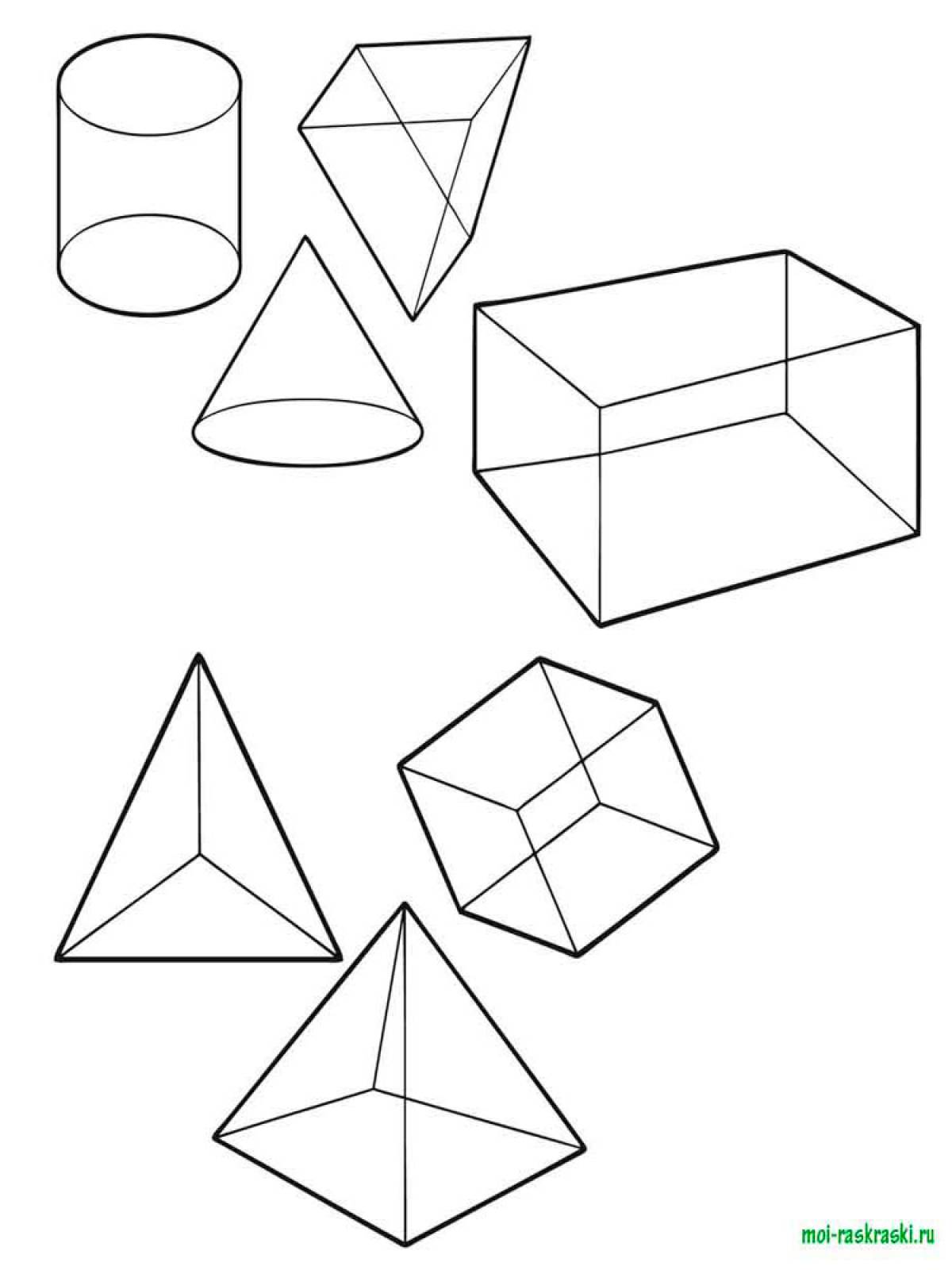
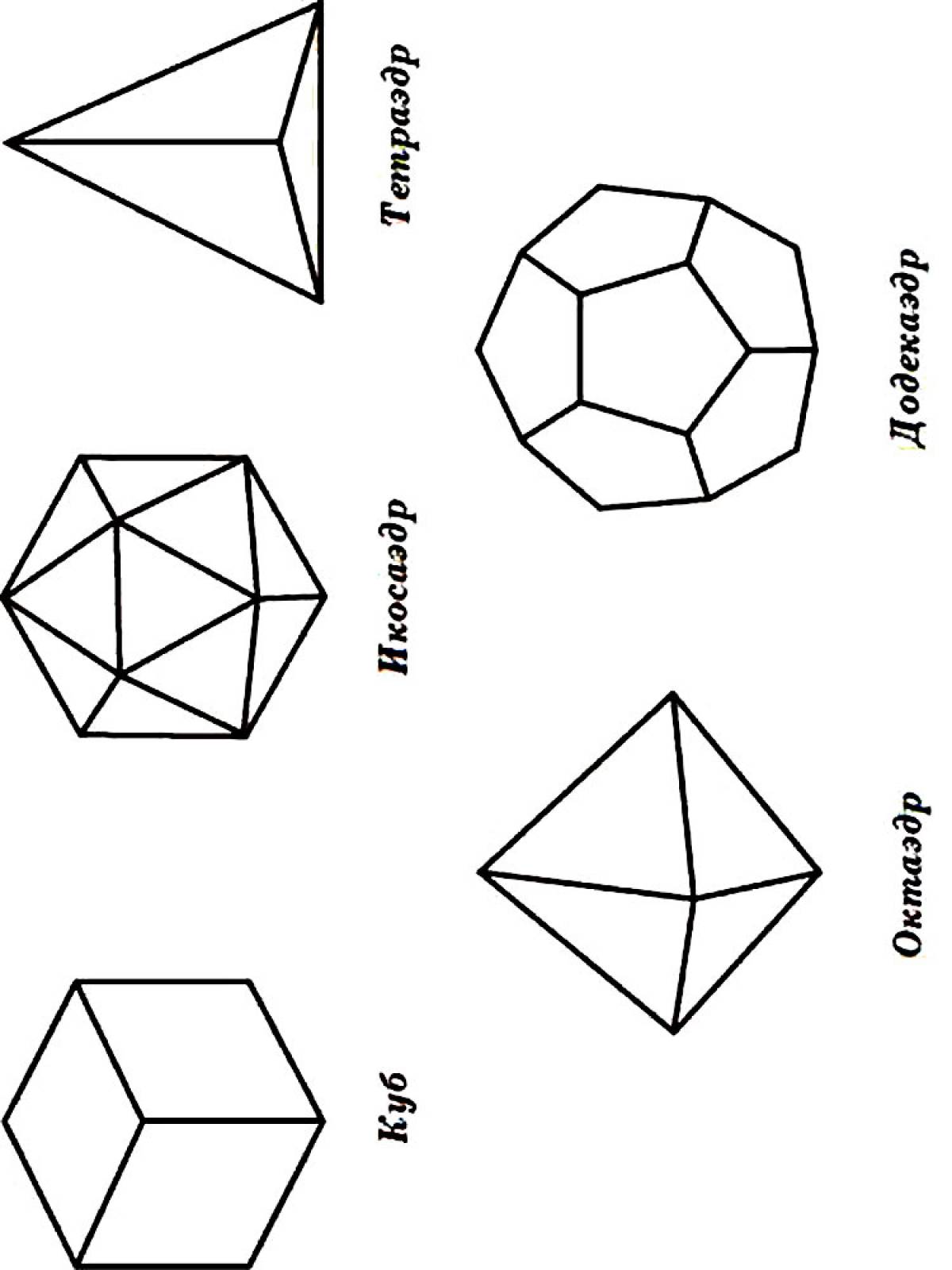
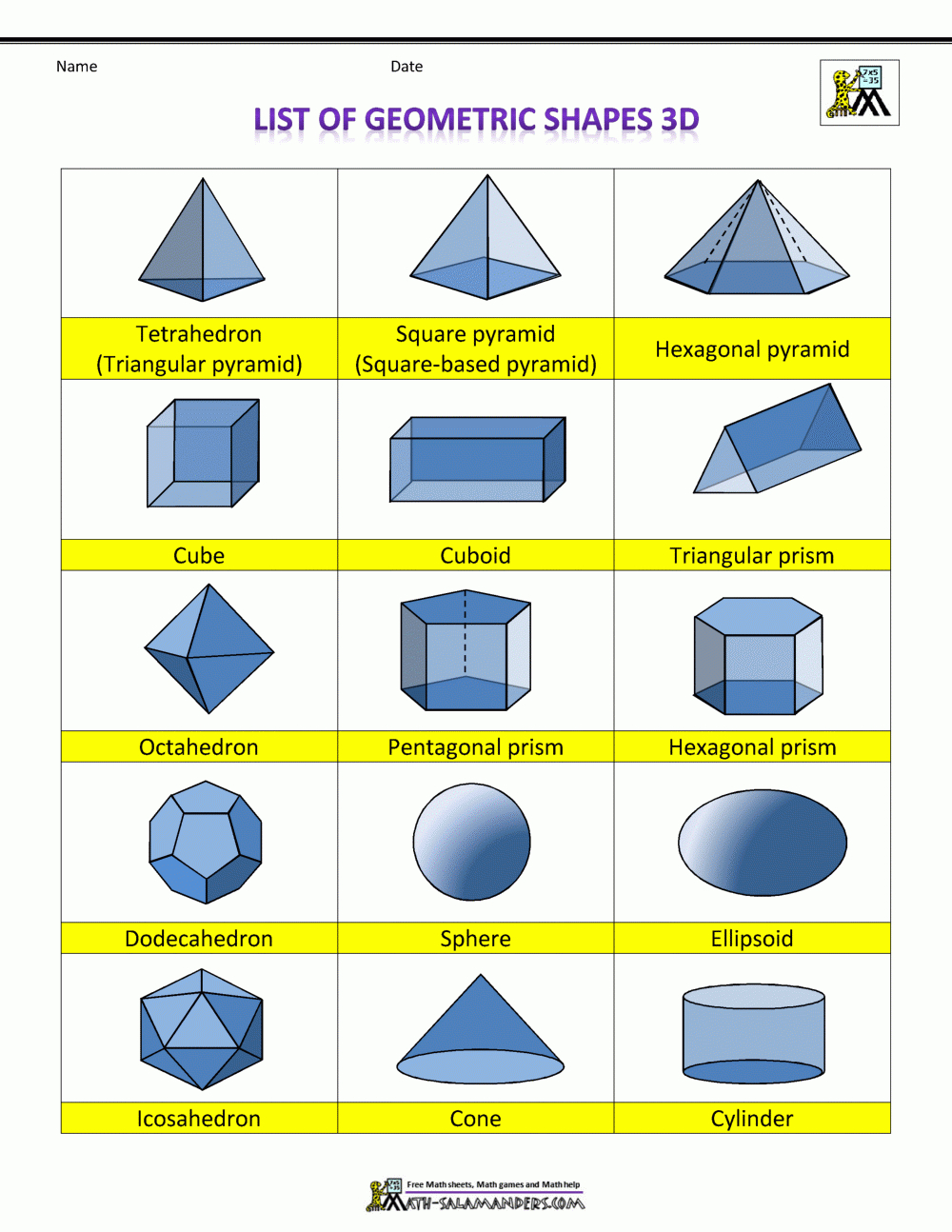
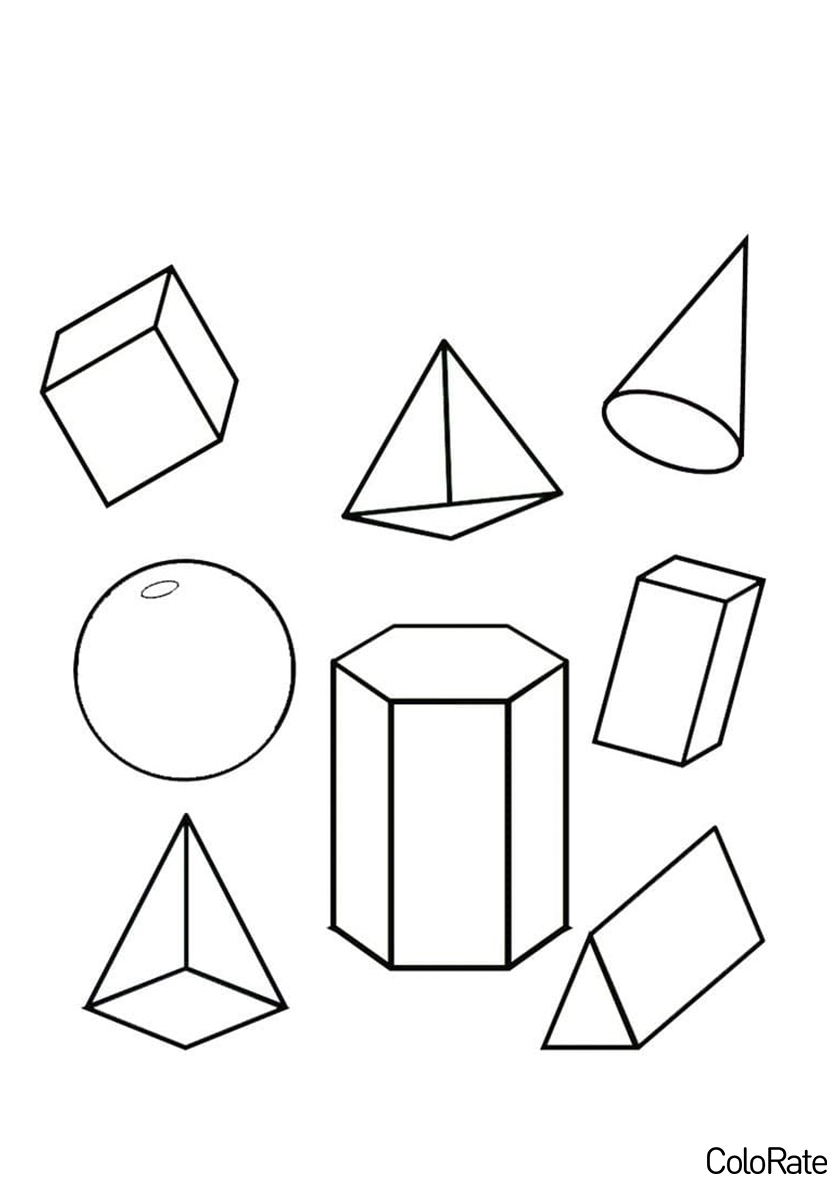
Объемные геометрические фигуры являются важной частью математики и геометрии. Они имеют трехмерную форму и обладают объемом, который можно вычислить с помощью специальных формул. К таким фигурам относятся куб, параллелепипед, пирамида, конус, цилиндр и шар. Каждая из них обладает своими уникальными свойствами и характеристиками.
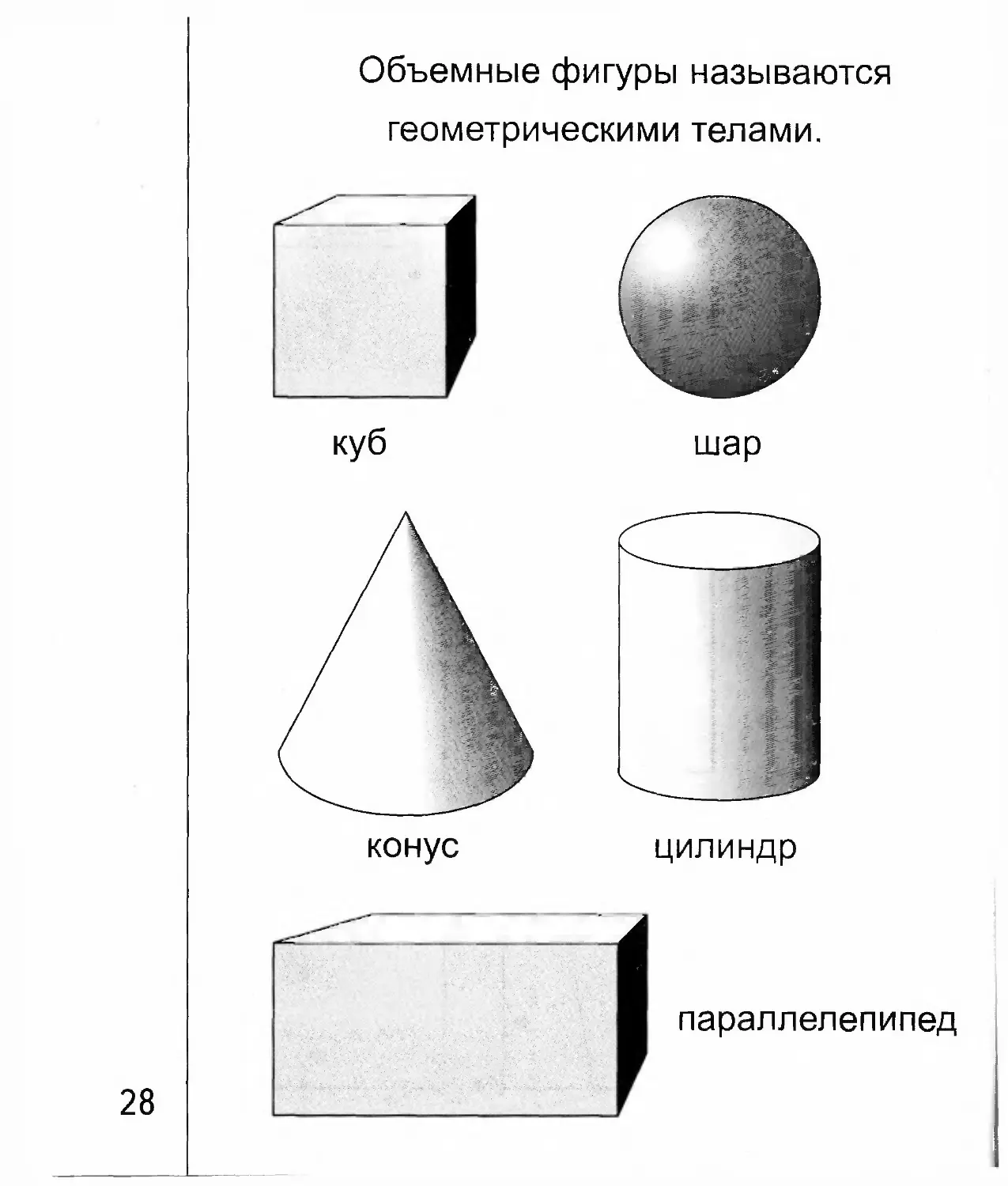
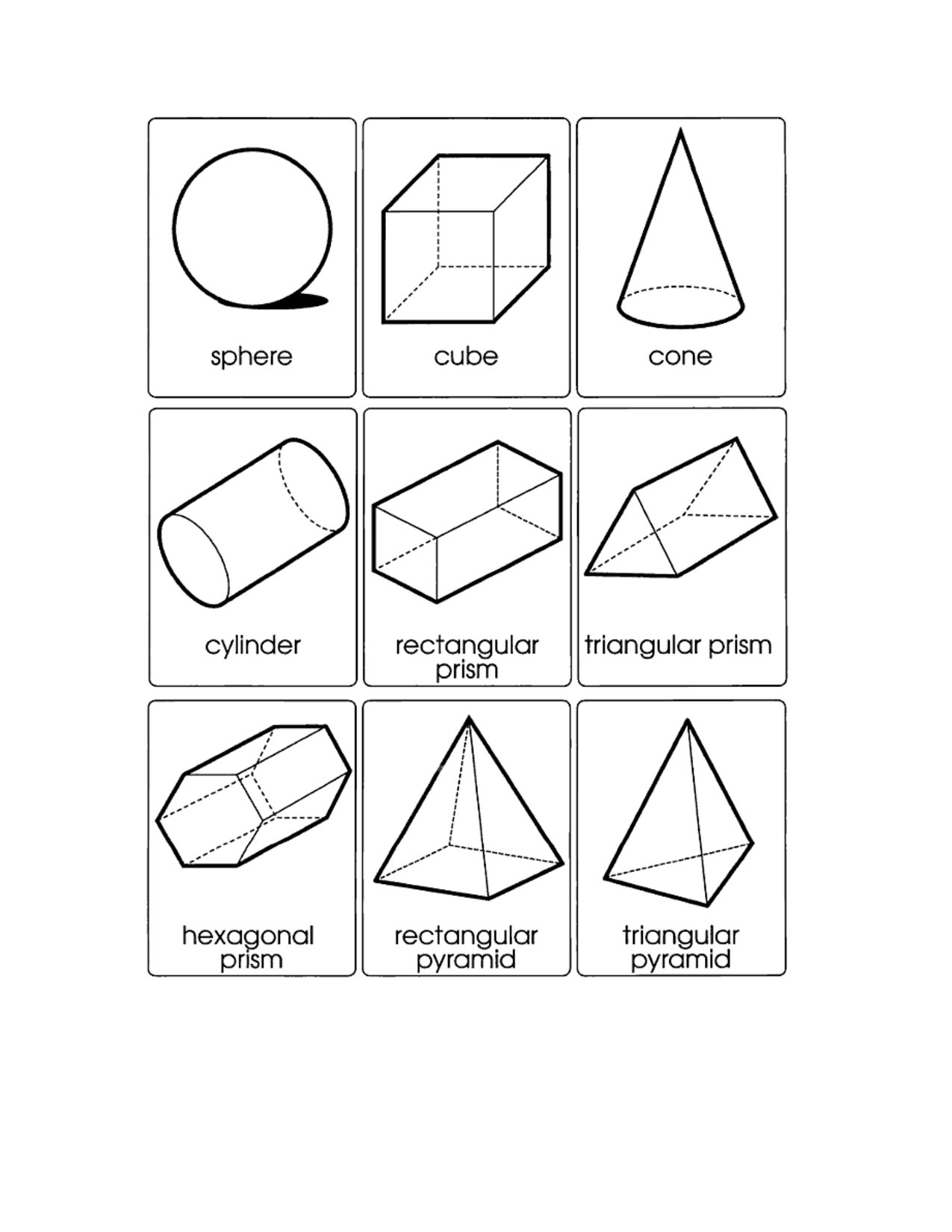
Одной из самых простых объемных геометрических фигур является куб. Он имеет шесть одинаковых граней, каждая из которых является квадратом. Объем куба можно найти, умножив длину его ребра в кубе. Параллелепипед, в свою очередь, имеет прямоугольную форму и также имеет шесть граней. Его объем вычисляется как произведение трех его сторон.





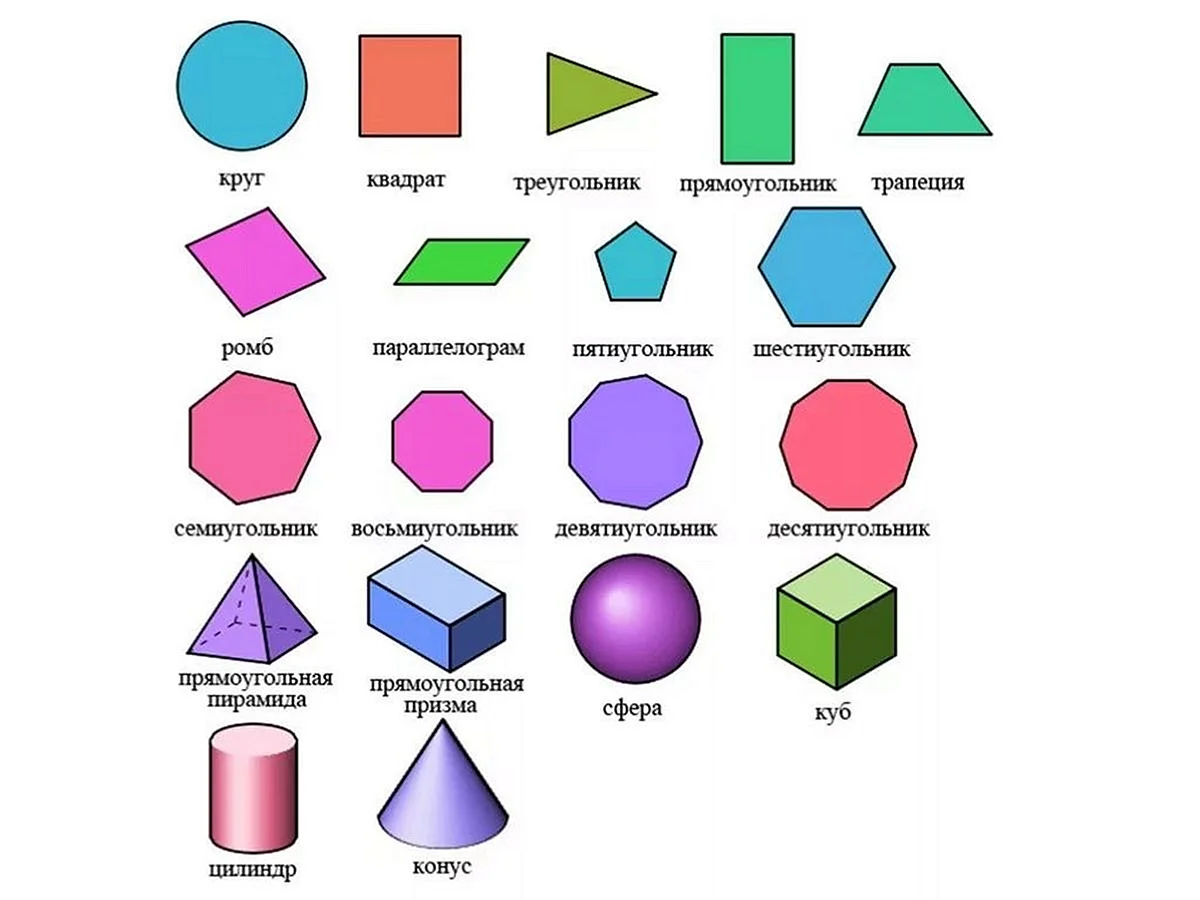
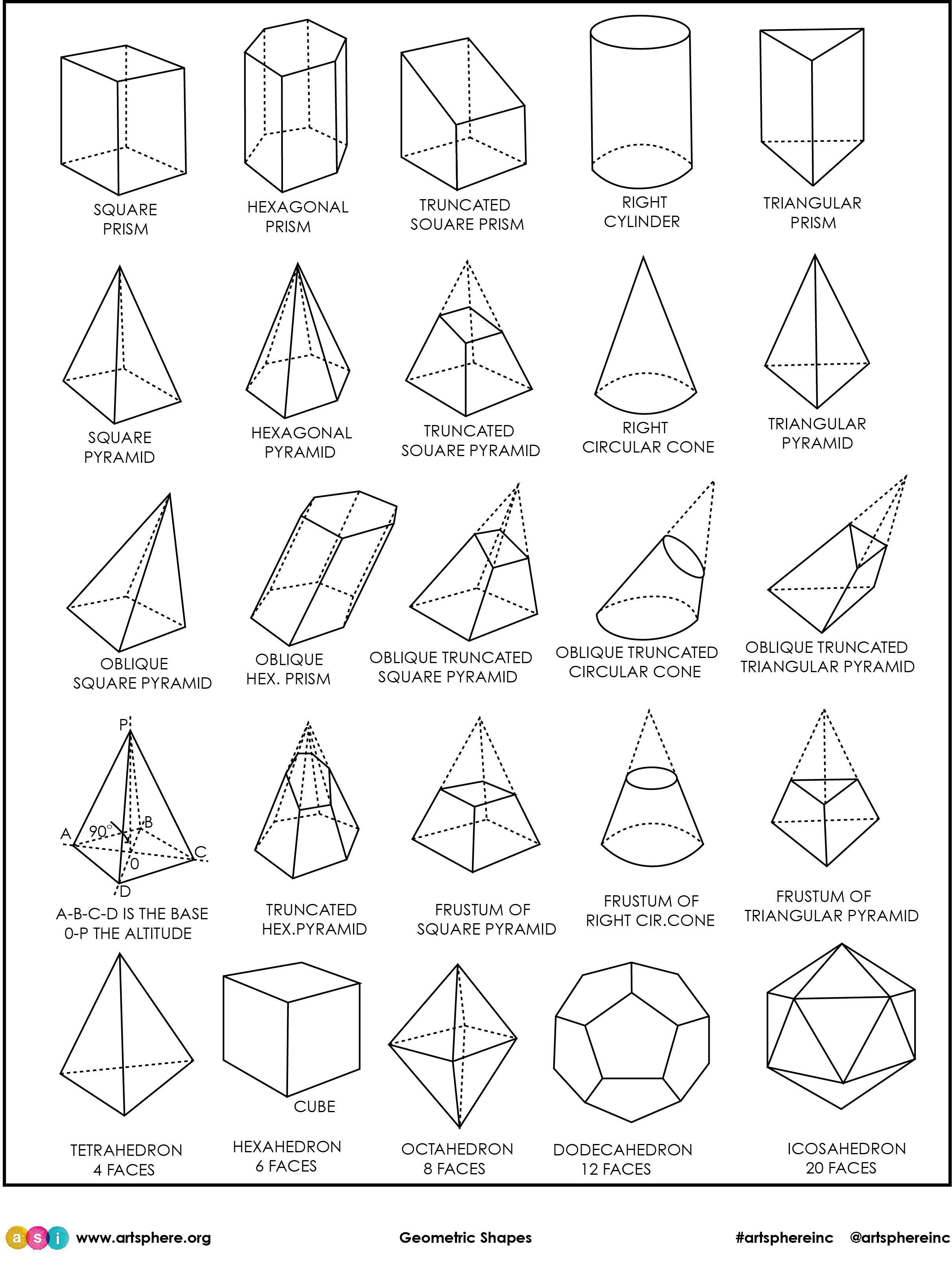



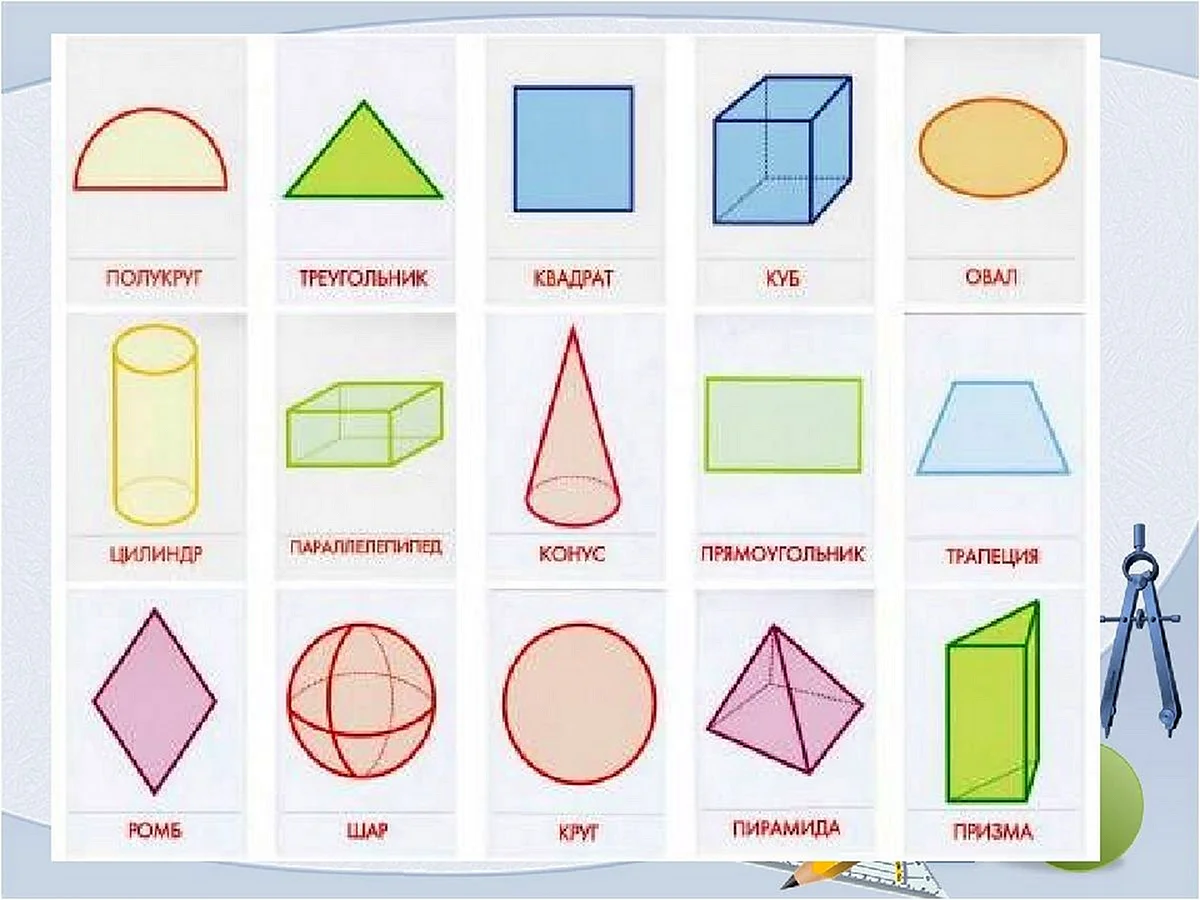




Исследуем пирамиду и конус
Пирамида - это геометрическое тело, у которого основание является многоугольником, а боковые грани - треугольниками, сходящимися в одной вершине. Объем пирамиды находится по формуле, которая зависит от формы ее основания. Конус же имеет круглое основание и боковую поверхность, образующуюся при вращении прямоугольного треугольника вокруг одного из катетов. Его объем можно вычислить по формуле, зависящей от радиуса основания и высоты.
Шар - это геометрическое тело, все точки которого находятся на одинаковом расстоянии от центра. Он не имеет граней и ребер, а его объем можно найти по формуле, зависящей от радиуса шара. Цилиндр представляет собой объемное тело, у которого два основания являются кругами, а боковая поверхность - прямоугольником. Его объем рассчитывается по формуле, зависящей от радиуса основания и высоты цилиндра.
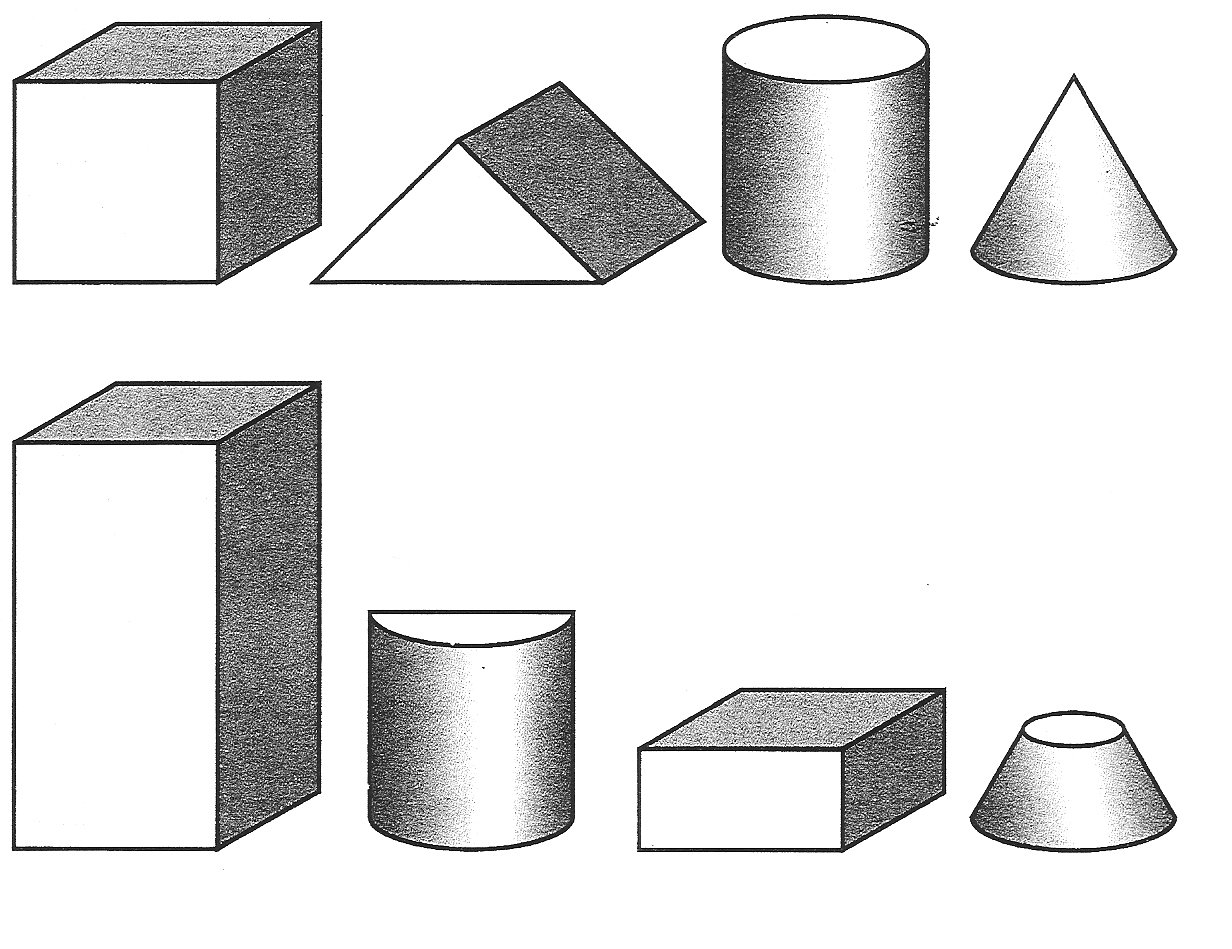

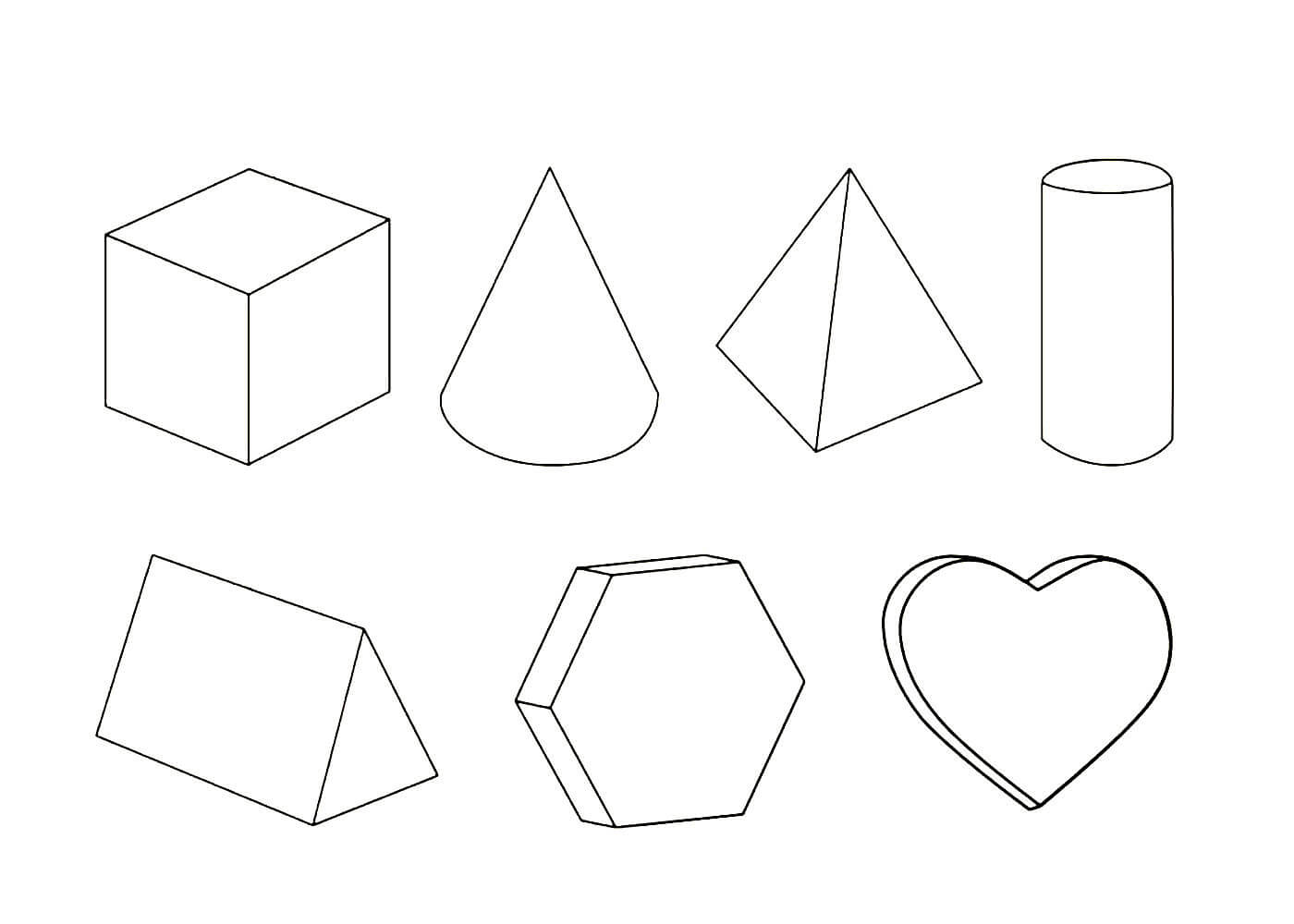

















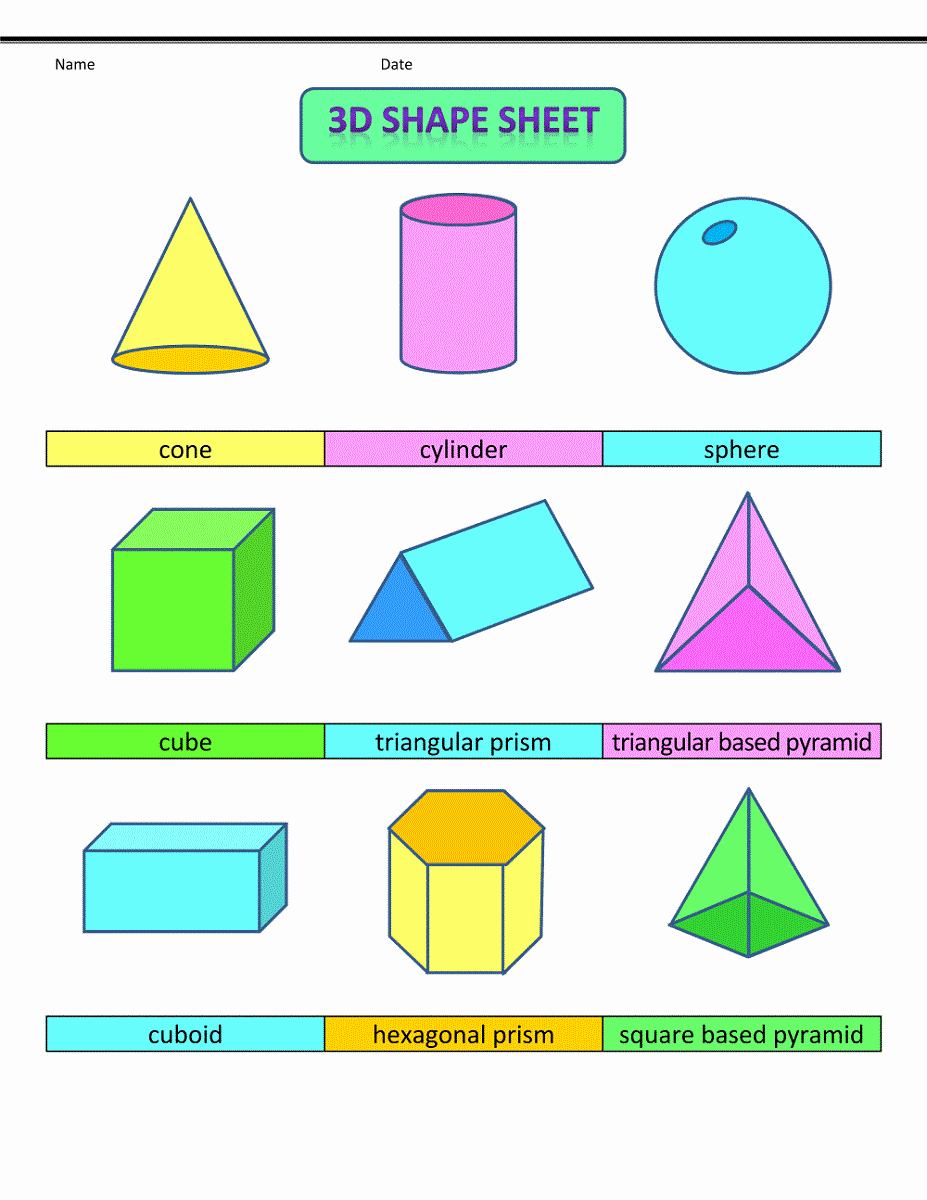

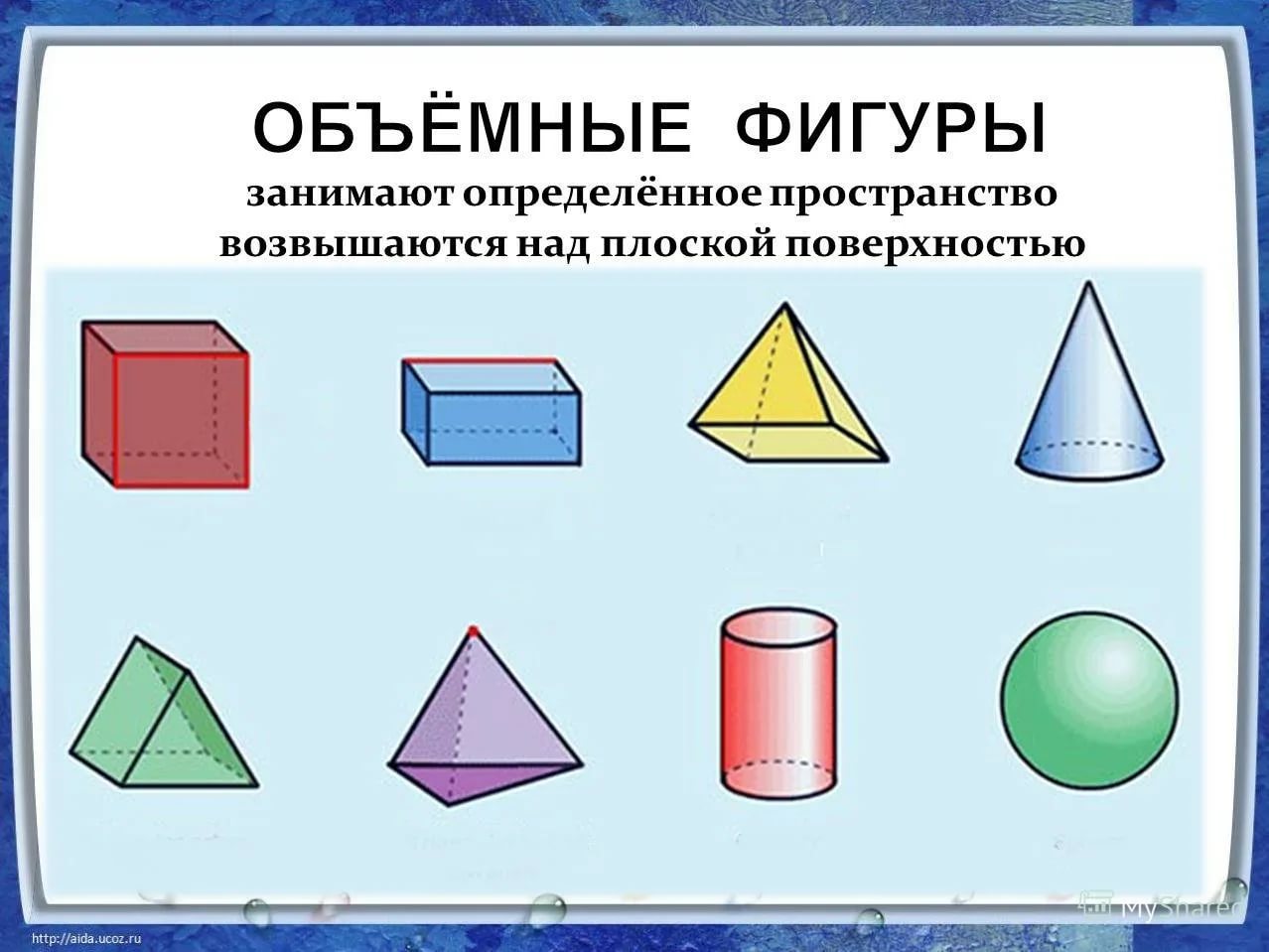

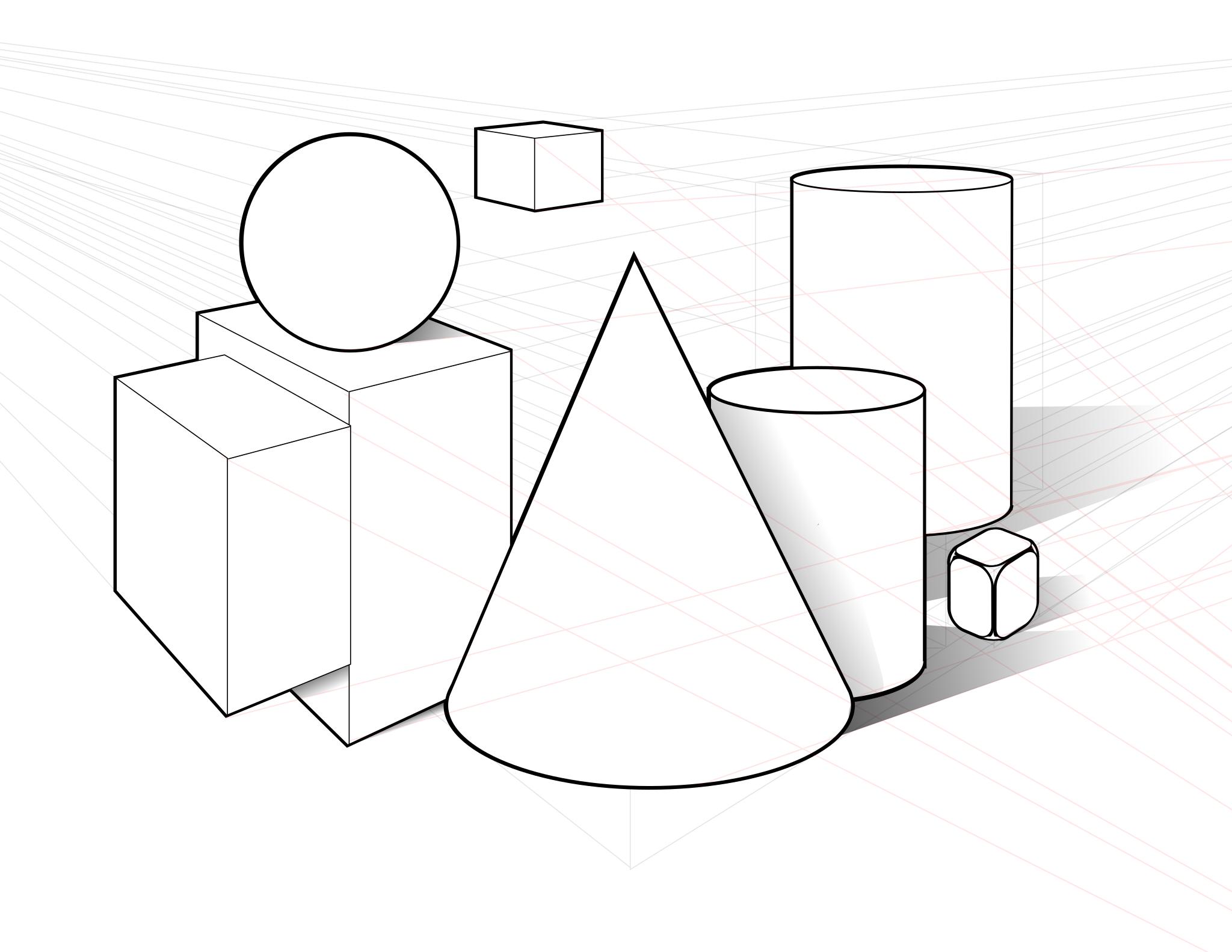


Изучаем свойства объемных геометрических фигур
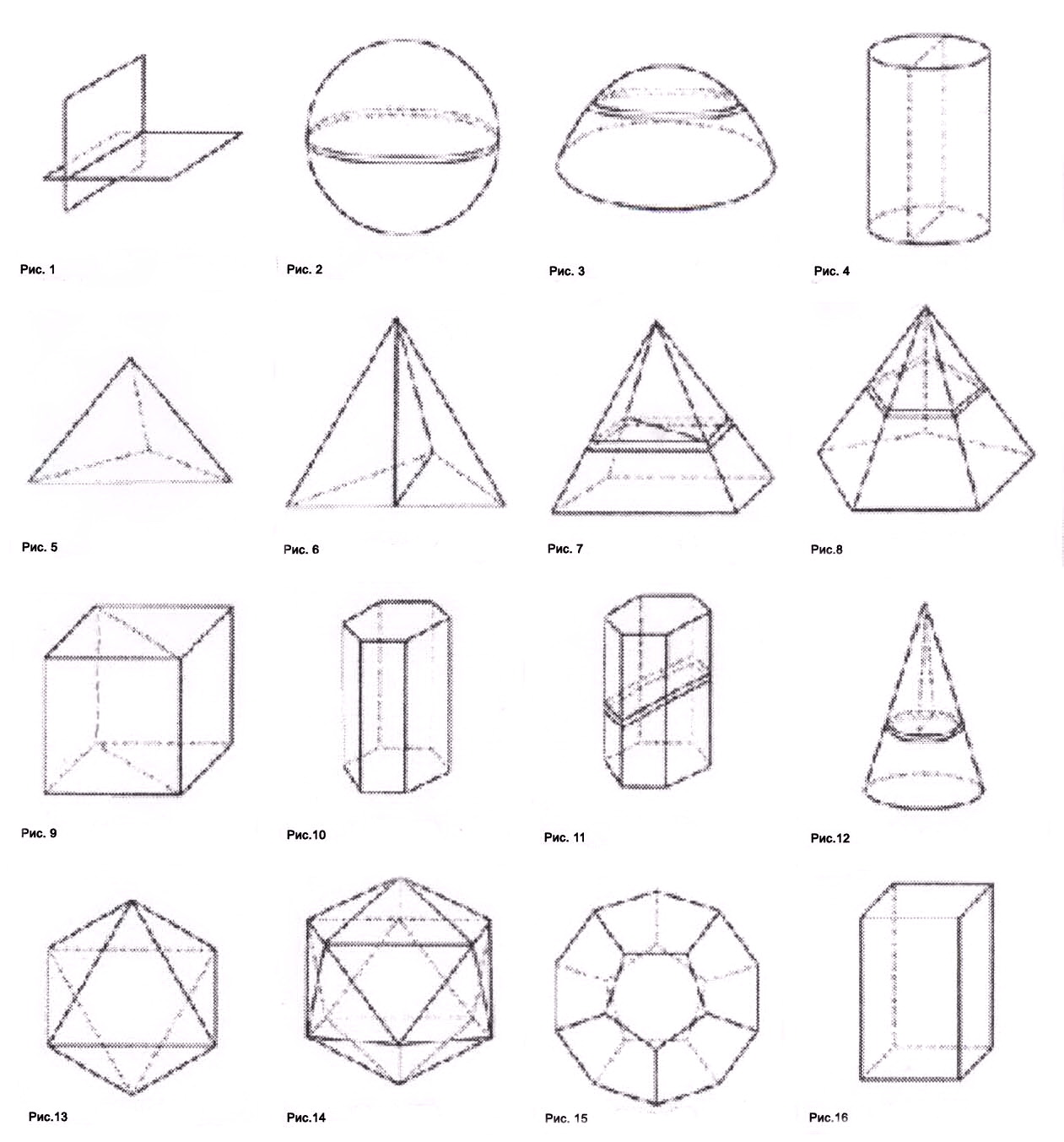
Каждая объемная геометрическая фигура обладает уникальными свойствами, которые определяют ее форму, объем и характеристики. Например, куб имеет все ребра одинаковой длины и все углы прямые. Параллелепипед может быть прямоугольным или квадратным, в зависимости от соотношения его сторон. Пирамида всегда имеет одну вершину, от которой отходят все боковые ребра.
Конус имеет одну вершину и круглое основание, а его боковая поверхность представляет собой образованную при вращении прямоугольного треугольника. Шар является самой совершенной геометрической фигурой, у которой радиус всех точек одинаков. Цилиндр имеет два круглых основания и прямоугольную боковую поверхность, которая соединяет их.













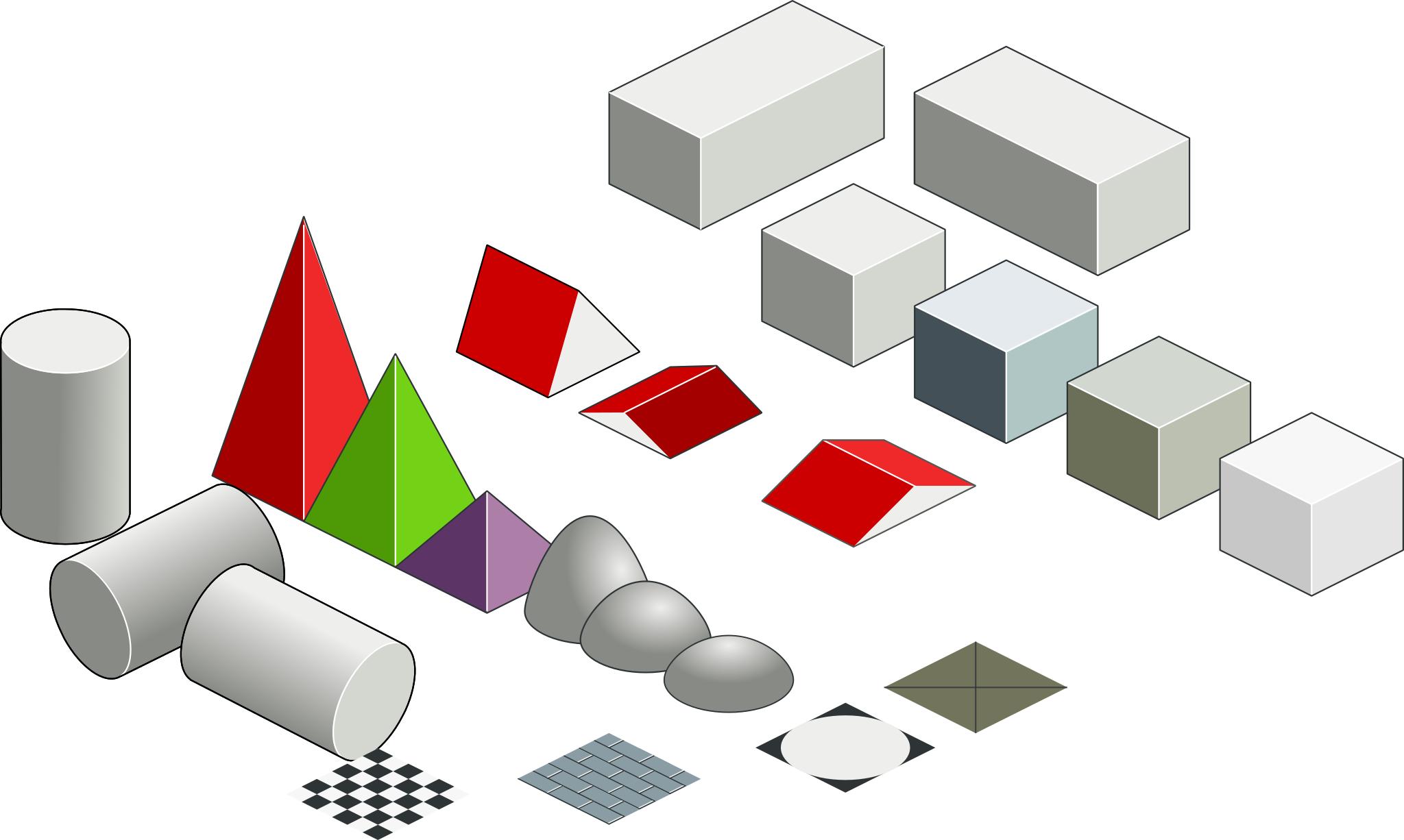












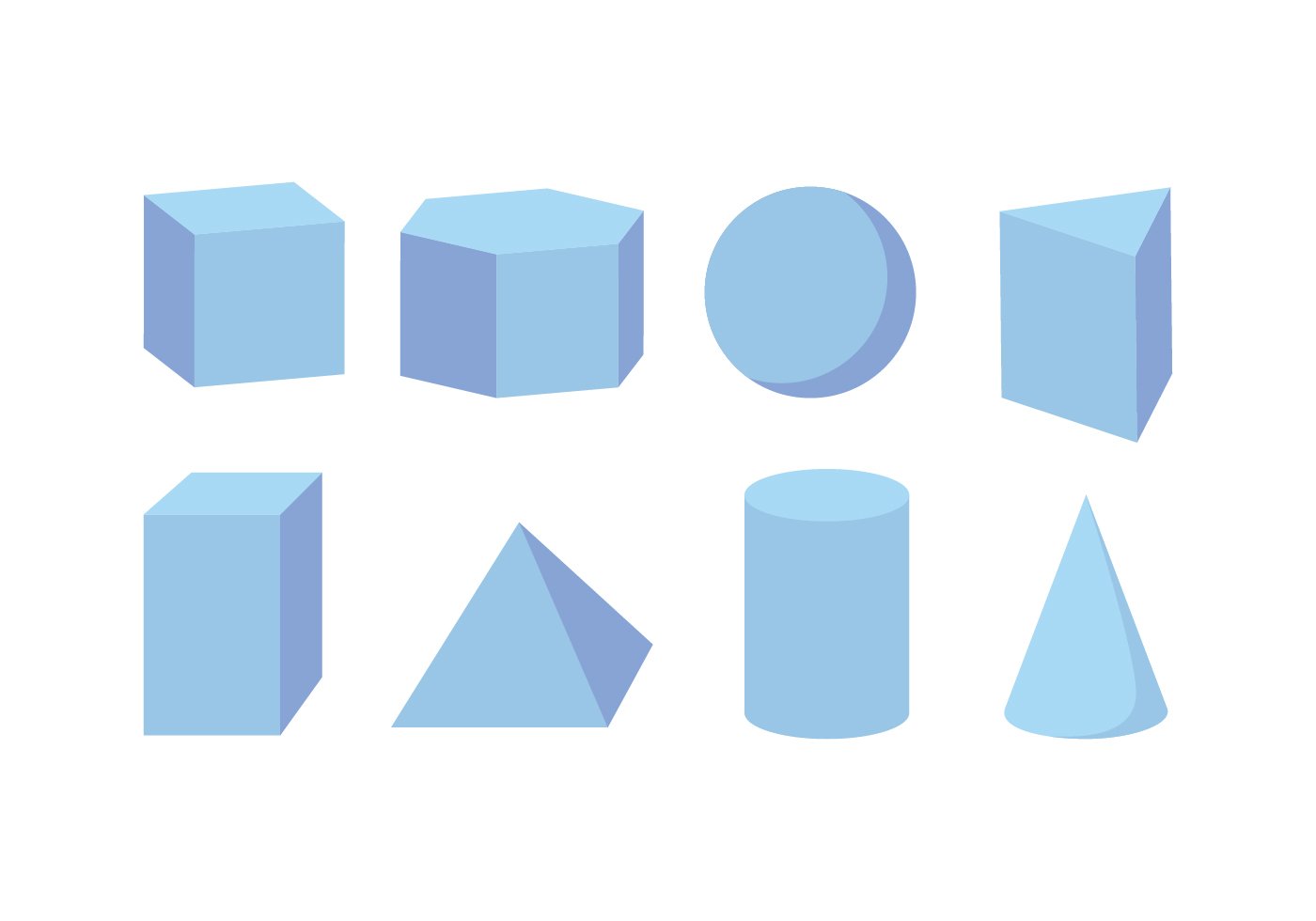
Визуализация объемных геометрических фигур
Изучение объемных геометрических фигур можно улучшить с помощью визуализации. Фотографии и изображения помогут лучше понять форму и структуру каждой фигуры, а также ее особенности. Различные ракурсы и перспективы позволят рассмотреть фигуры с разных сторон и оценить их объем.
Изучение объемных геометрических фигур - увлекательный и познавательный процесс, который позволяет погрузиться в мир математики и геометрии. Понимание свойств и характеристик каждой фигуры поможет лучше ориентироваться в пространстве и решать задачи, связанные с объемом и формой тел.
.Похожие стать:
- Тату геометрические цветы: искусство на вашем теле
- Идеи для дизайна ногтей в миндальной форме: новинки и геометрические узоры
- Как выбрать идеальные объемные обои для стен
- Неповторимые украшения: объемные броши из бисера
- Лучшие Объемные Дизайны Ногтей Фото: Вдохновение для Вашего Маникюра
- Как создать волшебные объемные локоны на длинные волосы
- Уют и красота: объемные обои с куроми
- Искусство Природы: Красивые объемные снежинки
- Объемные вязаные шапки для женщин: тепло и стиль в каждой детали
- Как стильно сочетать объемные кроссовки в женском гардеробе